Naive Bayes Classifier in Scikit-learn

December 22, 2021
No Comments
Machine Learning, Python, Scikit-learn

Before jumping into the details of Naive Bayes Classifier, let’s first understand what a classifier is.

The Classification Algorithm is a supervised learning technique that uses training data to determine the category of new observations. Classification is the process of machine learning (ML) from a dataset or observations, and then classifying fresh observations into one of several classes or groupings. Yes or No, 0 or 1, Spam or Not Spam, Cat or Dog, are such examples. Targets/labels or categories are all terms that can be used to describe classes.

There are two types of classifications:

  • Binary Classifier: This type of classifier is used when there are only two possible outputs to a classification task. Example – Yes/No, Male/Female, Spam/Not Spam, and so on
  • Multi-class Classifier: A Multi-class Classifier is used when a classification task involves more than two outcomes. Example – Classifications of different types of music, etc

Some types of ML classification algorithms:

What is Naive Bayes Classifier?

The Bayes Theorem is used to create a statistical classification approach known as Naive Bayes. It’s one of the most basic supervised learning algorithms out there. The Naive Bayes Classifier is a reliable, accurate and fast algorithm. On large datasets, it has great accuracy and speed.

The Naive Bayes Classifier implies that the influence of one characteristic in a class is independent of the effect of other features. For example, a loan applicant’s worth is determined by his or her income, prior loan, transaction history, age, and geography. Even though these traits are interrelated, they are nonetheless evaluated separately. Because this assumption makes calculation easier, it is regarded as naive. Class conditional independence is the term for this assumption.

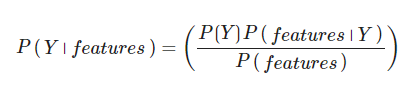
Naive Bayes Classifier
  • P(h): prior probability of h
  • P(h|D): posterior probability
  • P(D): prior probability of predictor
  • P(D|h): It is the likelihood which is the probability of predictor given class

Different Kinds Of Naive Bayes Classifiers

  • Gaussian Naive Bayes – The data from each label is assumed to be derived from a simple Gaussian distribution using the Gaussian Naive Bayes classifier
  • Multinomial Naive Bayes – The characteristics are assumed to be chosen from a basic Multinomial distribution
  • Bernoulli Naive Bayes – The model assumes that the features are binary (0s and 1s) in nature. Text classification with the ‘bag of words’ model is an application of Bernoulli Nave Bayes classification
  • Complement Naive Bayes – It was created to correct the Multinomial Bayes classifier’s severe assumptions. This type of NB classifier works well with unbalanced data sets

Building Naive Bayes Classifier

We can build a simple Naive Bayes Classifier using scikit-learn as shown below:

  • Loading needed libraries:

import pandas as pd, math, numpy as np
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

Naive Bayes Classifier
  • Let’s load one of the inbuilt datasets in sklearn library:

iris = load_iris()
X = iris.data
y = iris.target
y_labels = iris.target_names
X_labels = iris.feature_names

  • Let’s look at variables:

print(“Col_names – “,labels_X)
print(“X Shape – “,X.shape)
print(“Target(y) vals – “,labels_y)

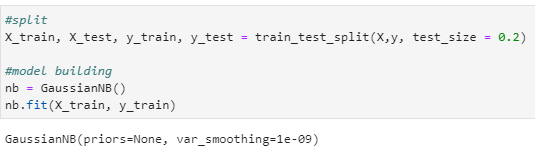
  • Let’s split the data and fit the data:

#split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size = 0.2)
#model building
nb = GaussianNB()
nb.fit(X_train, y_train)

Naive Bayes Classifier
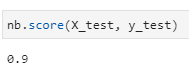
  • Let’s evaluate the model using test data:

nb.score(X_test, y_test)

The simple Naive bayes has performed well with a score of 0.9

Summary

Pros:

  • Predicting the test dataset’s class is simple and quick. It’s also good at multi-class prediction
  • When the assumption of independence is true, a Naive Bayes classifier outperforms other models such as logistic regression, and it requires less training data
  • When compared to numerical input variables, it performs well with categorical input variables (s)

Cons:

  • If a categorical variable in the test dataset has a category that was not included in the training data set, the model will assign a probability of 0 and will be unable to generate a prediction. This is called  “Zero Frequency.” We can use  Laplace estimation as a way to avoid this issue. Laplace estimation is one of the basic smoothing techniques out there
  • The assumption of independent predictors is another flaw in Naive Bayes since in real life, getting a collection of predictors that are totally independent is nearly impossible

References

Tags: , , , ,